兰贝特定律及红外测温瞄准方向
兰贝特定律,又称之为余弦定律。
从兰贝特定律指出了黑体辐射能量在空间的分布规律,同时也说明了红外测温需要遵循的测温瞄准方向。
基本问题
经常我们会碰到客户问,用红外测温仪或红外热像仪测量一个物体的温度,应该怎么安装红外测温仪或红外热像仪呢?
换言之,就是怎么安装红外测温仪或红外热像仪,和被测物体之间的角度是多少,才能准确测温呢?
黑体辐射的基本规律
我们可以从相关书籍上很容易找到这些热辐射和黑体辐射的基本规律和特性:
1. 斯忒藩-玻耳兹曼定律:
黑体的辐射力由斯忒藩-玻耳兹曼定律来确定,辐射力与温度T的四次方成正比:
斯忒藩-玻耳兹曼定律计算的是绝对黑体表面所辐射的总能量。
2. 普朗克定律
黑体辐射能量按波长的分布服从普朗克定律。
3. 兰贝特定律
黑体辐射能量按空间方向的分布服从兰贝特定律;
4. 维恩位移定律:
黑体的光谱辐射力有一个峰值,与此峰值值相对应的波长λm由维恩位移定律确定;随着温度的升高,λm向波长短的方向移动。
兰贝特定律(余弦定律)
平面几何中,通常用平面角来表示某一方向的空间所占的大小,其单位为弧度。类似地,在三维空间中,用立体角(solid angle)Ω及微元立体角dΩ来表示某一方向的空间所占的大小,
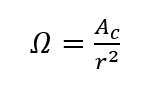 (1)
(1)
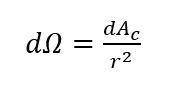 (2)
(2)
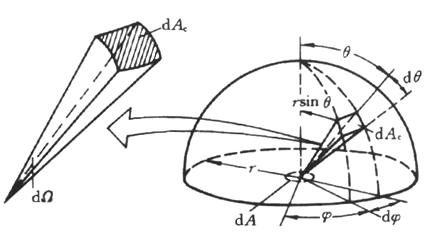
图1:微元立体角和半球空间几何参数的关系
上图中,φ为经度角(azimuthal angle), θ为纬度角(latitudinal angle)。r为半球半径,Ac为Ω对应的面积,dAc为dΩ对应的微面积。
空间的方向可以用该方向的经度角与纬度角来表示。
显然,要说明黑体向半球空间辐射出去的能量按不同方向分布的规律,只有对不同方向的相等的立体角来比较才有意义。
立体角的单位称为空间度,通常记为sr。
 (3)
(3)
这个公式是实验测定的。它表明,面积为dA的黑体微元面积向围绕空间纬度角θ方向的微元立体角dΩ内辐射出去的能量为dΦ(θ)。
这里I为常数,与θ方向无关。这个公式还可以表达为:
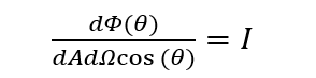 (4)
(4)
这里dAcosθ可以视作从θ方向看过去的面积,称为可见面积。参见下图:
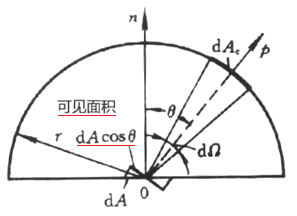
上式左侧物理量是从黑体(炉)单位可见面积发射出去的落到空间任意方向的单位立体角中的能量,称之为定向辐射强度(Directional radiation intensity)。
式(4)表明黑体的定向辐射强度是个常量,与空间方向无关。这就是黑体辐射的兰贝特定律。
注意,定向辐射强度是以单位可见面积作为度量依据的,如果以单位实际辐射面积为度量依据,则就是式(3)所示的结果。该式表明,黑体单位面积辐射出去的能量在空间的不同方向分布是不均匀的,按空间纬度角θ的余弦规律变化;在垂直于该表面的方向最大,而与表面平行的方向为零,这是兰贝特定律的另一种表达方式,称为余弦定律。
这就告诉我们,要采用红外测温仪、红外扫描热像仪、红外热像仪对红外辐射进行测温,那么瞄准被测物体或辐射体的方向,需遵循兰贝特定律。换言之,
最准确的测量瞄准方式,就是将红外镜头垂直于被测物体或辐射体(在垂直于该表面的方向最大);
越是与被测物体或辐射体的方向平行,获得的辐射能量就越小(而与表面平行的方向为零);
而其它瞄准方向所获得的红外能量和纬度角θ的余弦值cos(θ)相关。
兰贝特定律(Lambert Law),又称之为余弦定律,又翻译成朗伯定律。